
Competitive challenges are an integral part of the game of Survivor. They allow a player (or tribes of players) to earn safety and rewards within the game. In certain circumstances, challenges are used to determine when a player is eliminated or has earned their way back into the game. Each specific challenge has a unique set of circumstances that must be accounted for to properly contextualize the challenge performance rate. This is accomplished by calculating the marginal change (increase or decrease) between the actual wins and the probable win rates. The probable win rate is calculated by taking the number of players competing divided by the number of wins available. The underlying assumption is that the probable win rate is equal to the likelihood of a player winning a challenge if the challenge winner was completely random. By calculating the marginal difference between the probable win rate and the actual wins, a player's ability to win challenges can be measured.
Below are eight different challenges where challenge performance is calculated for each of the players. The eight examples were selected because they constitute different win totals, due to either being challenges between tribes, individuals or a combination of both. This demonstrates how the challenge performance set-up affect the context of each particular challenge and individual player.
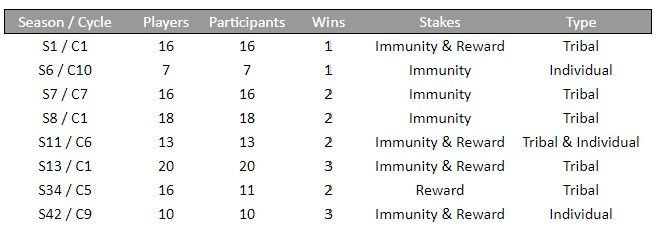
Example #1 – Season 1, Cycle 1:
# of players in the game = 16
# of players participating in challenge = 16
# of wins available = 1
Stakes = Immunity & Reward
Type = Tribal
This was a challenge between two tribes, each with eight players participating per tribe. Each participating player had a probable win share of 6.25%. For example, Kelly's probable win share was calculated by taking the total wins available and dividing by the number of tribes that could win (1 / 2 = .5000) and multiplying that by the number of participating players per tribe who would evenly share the win (1 / 8 = .1250). .5000 x .1250 = .0625.
A player who won received .1250 win shares for the challenge. For example, Colleen's marginal win difference was .0625 for this challenge (.1250 win shares - .0625 probable win shares). A loss resulted in zero win shares. Kelly had a negative marginal win difference of -.0625 for this challenge (.0000 win shares - .0625 probable win shares).
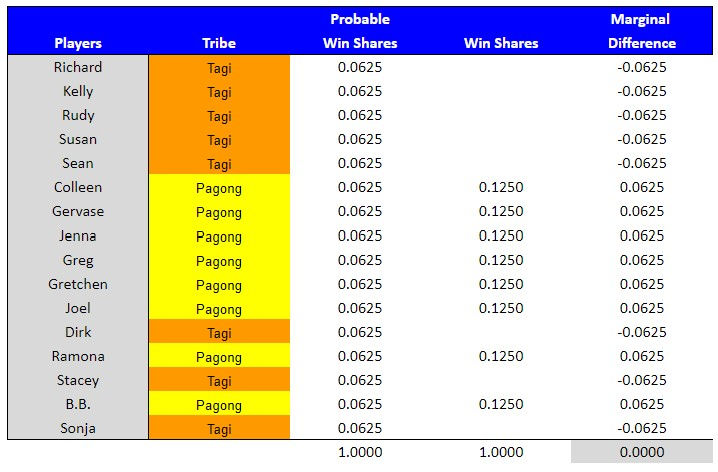
Example #2 – Season 6, Cycle 10:
# of players in the game = 7
# of players participating in challenge = 7
# of wins available = 1
Stakes = Immunity
Type = Individual
This was a challenge between seven individuals, Each participating player had a probable win share of 14.29%. For example, Jenna's probable win share was calculated by taking the total wins available and dividing by the number of players that could win (1 / 7 = .1429).
The player who won received 1 full win share for the challenge. For example, Rob's marginal win difference was .8571 for this challenge (1 win share - .1429 probable win shares). A loss resulted in zero win shares. Jenna had a negative marginal win difference of -.1429 for this challenge (.0000 win shares - .1429 probable win shares).
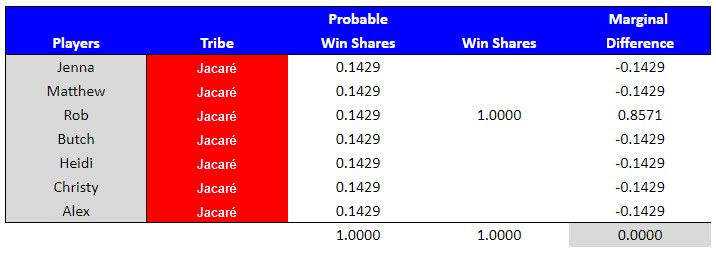
Example #3 – Season 7, Cycle 7:
# of players in the game = 16
# of players participating in challenge = 16
# of wins available = 2
Stakes = Immunity (Outcast tribe could win a chance to have 1 or 2 players return)
Type = Tribal
This was a challenge between three tribes, two of which had five players participating each (Drake and Morgan). Instead of the tribes competing against each other, they each were competing against the Outcast tribe, which was comprised of all the players that had been voted out up to that point in the game. Each participating player (on Drake and Morgan) had a probable win share of 10.00%. For example, Sandra's probable win share was calculated by taking the total wins available (for her tribe) and dividing by the number of tribes that could win (1 / 2 = .5000) and multiplying that by the number of participating players on her tribe who would evenly share the win (1 / 5 = .2000). .5000 x .2000 = .1000.
The Outcast tribe had the opportunity to win against one or both of the other tribes (which meant either no one, one or two players would return to the game). Each participating player on the Outcasts had a probable win share of 16.67%. For example, Burton's probable win share was calculated by taking the total wins available and dividing by the number of times the Outcasts could win (2 /2 = 1.0000) and multiplying that by the number of participating players on his tribe who would evenly share the win (1 / 6 = .1667). .1.0000 x .1667 = .1667.
A player who won received .3333 win shares (2 wins * .1667 win shares) for the challenge. For example, Burton's marginal win difference was .1667 for this challenge (.3333 win shares - .1667 probable win shares). A loss resulted in zero win shares. Sandra had a negative marginal win difference of -.1000 for this challenge (.0000 win shares - .1000 probable win shares).
Example #4 – Season 8, Cycle 1:
# of players in the game = 18
# of players participating in challenge = 18
# of wins available = 2
Stakes = Immunity
Type = Tribal
This was a challenge between three tribes, each with six players participating per tribe. Each participating player had a probable win share of 11.11%. For example, Amber's probable win share was calculated by taking the total wins available and dividing by the number of tribes that could win (2 / 3 = .6667) and multiplying that by the number of participating players per tribe who would evenly share the win (1 / 6 = .1667). .6667 x .1667 = .1111.
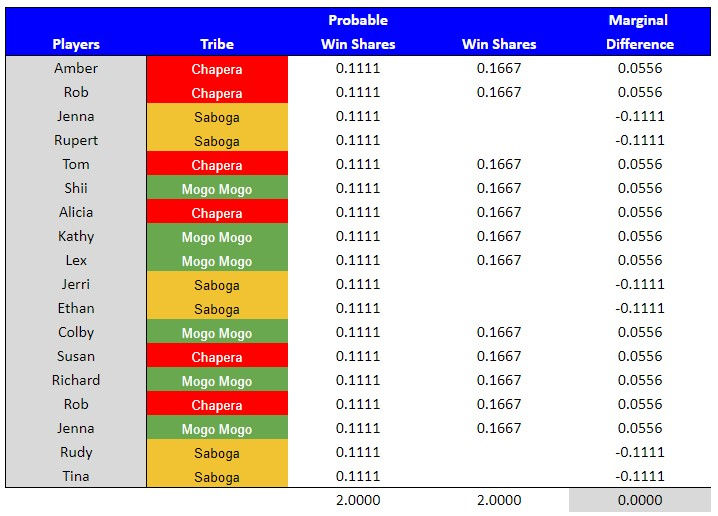
A player who won received .1667 win shares for the challenge. For example, Amber's marginal win difference was .0556 for this challenge (.1667 win shares - .1111 probable win shares). A loss resulted in zero win shares. Rupert had a negative marginal win difference of -.1111 for this challenge (.0000 win shares - .1111 probable win shares).
Example #5 – Season 11, Cycle 6:
# of players in the game = 13
# of players participating in challenge = 13
(Yaxhá = 6 & Nakúm = 5 in tribal phase and Nakúm = 7 in individual phase)
# of wins available = 2
Stakes = Immunity & Reward
Type = Tribal & Individual
This was a challenge between two tribes for tribal immunity, with the winning tribe then able to compete individually for a reward. The Yaxhá tribe's players had a probable win share of 16.03%. For example, Danni's probable win share for the tribal phase was calculated by taking the total wins available and dividing by the number of tribes that could win (1 / 2 = .5000) and multiplying that by the number of participating players per tribe who would evenly share the win (1 / 6 = .1667). .5000 x .1667 = .0833. Danni's probable win share for the individual phase was calculated by taking the total wins available and dividing by the number of players that could win (1 /13 = .0769). Danni's total probable win shares for both phases is the sum of both the tribal and individual phases (.0833 + .0769 = .1603).
The Nakúm tribe's participating players had a probable win share of 17.69%. For example, Stephenie's probable win share for the tribal phase was calculated by taking the total wins available and dividing by the number of tribes that could win (1 / 2 = .5000) and multiplying that by the number of participating players per tribe who would evenly share the win (1 / 5 = .2000). .5000 x .2000 = .1000. Stephenie's probable win share for the individual phase was calculated by taking the total wins available and dividing by the number of players that could win (1 /13 = .0769). Stephenie's total probable win shares for both phases is the sum of both the tribal and individual phases (.1000 + .0769 = .1769).
The Nakúm tribe had two players who did not participate in the tribal phase of the challenge (Rafe & Lydia), but because Nakúm won the tribal phase, they were both allowed to compete in the individual phase. For example, Rafe's probable win share for the individual phase was calculated by taking the total wins available and dividing by the number of players that could win (1 /13 = .0769).
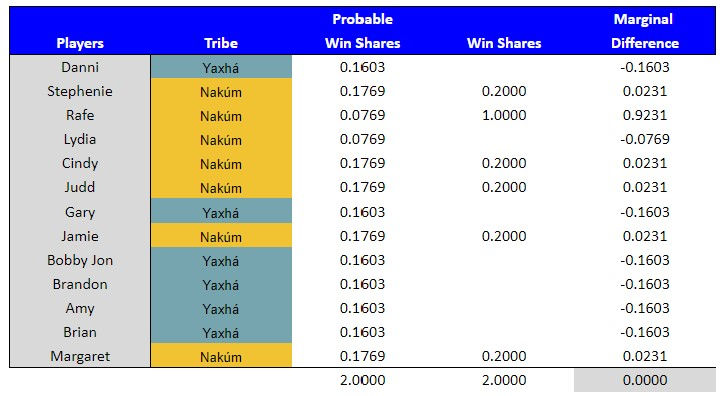
Since Nakúm won, a participating player received .2000 win shares for the tribal phase of the challenge. The player who won the individual phase received 1 full win share for the challenge. For example, Rafe's marginal win difference was .9231 for this challenge (1 win share - .0769 probable win shares) since he only competed in the individual phase. Stephenie, who competed in both the tribal and individual phases had a marginal win difference of .0231 for both phases of the challenge ((.2000 win shares + .0000 win shares) - .1769 probable win shares). A loss resulted in zero win shares. Lydia had a negative marginal win difference of -.0769 for the individual challenge (.0000 win shares - .0769 probable win shares).
All six players on the Yaxhá tribe lost both the tribal and individual phases (they lost the individual phase by default because they didn't qualify to participate). A loss resulted in zero win shares. Danni has a negative marginal win difference of -.1603 for both phases of the challenge ((.0000 win shares + .0000 win shares) - .1603 probable win shares).
Example #6 – Season 13, Cycle 1:
# of players in the game = 20
# of players participating in challenge = 20
# of wins available = 3
Stakes = Immunity & Reward
Type = Tribal
This was a challenge between four tribes, each with five players participating per tribe. Each participating player had a probable win share of 15.00%. For example, Yul's probable win share was calculated by taking the total wins available and dividing by the number of tribes that could win (3 / 4 = .7500) and multiplying that by the number of participating players per tribe who would evenly share the win (1 / 5 = .2000). .7500 x .2000 = .1500.
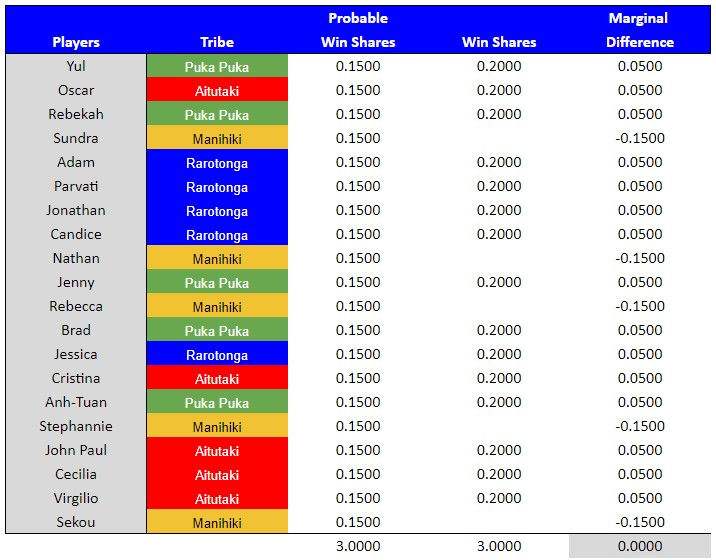
A player who won received .2000 win shares for the challenge. For example, Yul's marginal win difference was .0500 for this challenge (.2000 win shares - .1500 probable win shares). A loss resulted in zero win shares. Sundra had a negative marginal win difference of -.1500 for this challenge (.0000 win shares - .1500 probable win shares).
Example #7 – Season 34, Cycle 5:
# of players in the game = 16
# of players participating in challenge = 11
(Tavua = 5, Mana = 1, & Nuku = 5)
# of wins available = 2
Stakes = Reward
Type = Tribal
This was a challenge between three tribes, each with five players participating per tribe. Although five players per tribe started the challenge, Debbie (Mana tribe) was unable to complete a section of the obstacle course, therefore preventing the rest of her tribe from proceeding to the next stage of the challenge. As such, it was determined that only Debbie was a participant and the rest of her tribe were scored as if they didn't participate in the challenge. Each participating player (for Tavua and Nuku) had a probable win share of 13.33%. For example, Sarah's probable win share was calculated by taking the total wins available and dividing by the number of tribes that could win (2 / 3 = .6667) and multiplying that by the number of participating players per tribe who would evenly share the win (1 / 5 = .2000). .6667 x .2000 = .1333.
As the lone official participant from the Mana tribe, Debbie's probable win share was calculated by taking the total wins available and dividing by the number of tribes that could win (2 / 3 = .6667) and multiplying that by the number of participating players in her tribe who would evenly share the win (1 / 1 = 1.0000). .6667 x 1.0000 = .6667.
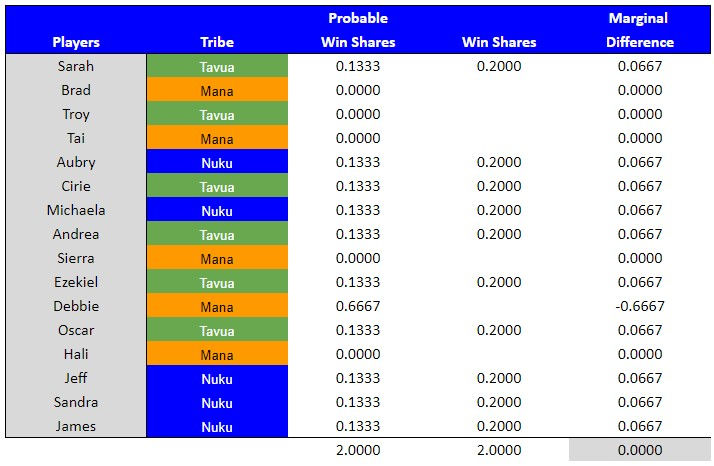
A player who won received .2000 win shares for the challenge. For example, Sarah's marginal win difference was .0667 for this challenge (.2000 win shares - .1333 probable win shares). A loss resulted in zero win shares. Debbie had a negative marginal win difference of -.6667 for this challenge (.0000 win shares - .6667 probable win shares).
Example #8 – Season 42, Cycle 9:
# of players in the game = 10
# of players participating in challenge = 10
# of wins available = 3
Stakes = Immunity & Reward
Type = Individual
This was a challenge between ten individuals that were divided into two tribes, where they competed both against their own tribemates for immunity and against the entire group for a reward. Each participating player had a probable win share of 30.00%. For example, Maryanne's probable win share for the immunity phase was calculated by taking the total wins available and dividing by the number of players that could win (1 / 5 = .2000). Maryanne's probable win share for the reward phase was calculated by taking the total wins available and dividing by the number of players that could win (1 /10 = .1000). Maryanne's total probable win shares for both phases is the sum of both the immunity and reward phases (.2000 + .1000 = .3000).
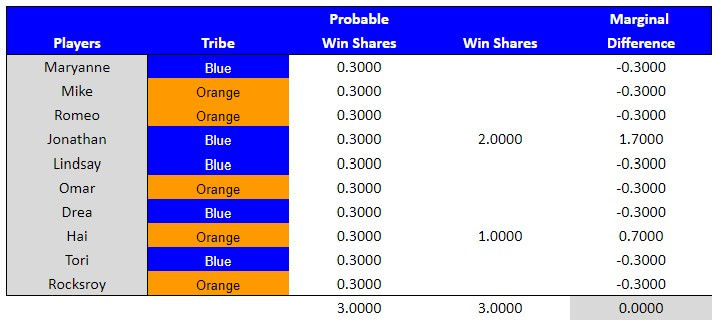
A player who won the immunity phase received 1 full win share for the challenge. For example, Hai's marginal win difference was .7000 for this challenge (1 win share - .3000 probable win shares). Jonathan, who won both the immunity and reward phases had a marginal win difference of 1.7000 for both phases of the challenge ((1 win share + 1 win share) - .3000 probable win shares). A loss resulted in zero win shares. Mike had a negative marginal win difference of -.3000 for the individual challenge (.0000 win shares - .3000 probable win shares).
Individual Challenge Performance per Game:
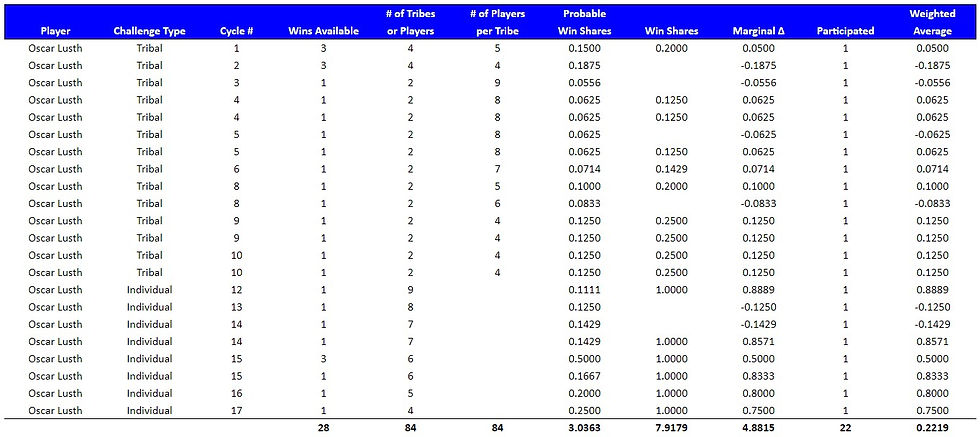
A player's total challenge performance for the season can be calculated by adding their individual challenge performance together. For example, Oscar Lusth (2nd place in season 13) had a challenge performance rate of .2219 across twenty-two challenges. He was able to win sixteen times, which is a total of 7.9179 win shares. His marginal win rate was 4.8815 (7.9179 - 3.0363). His weighted average for the season was .2219 (4.8815 / 22).
Marginal Rate vs. Raw Rate:
A final consideration for why the marginal rate is calculated vs. just the raw rate. If there are two players with the same raw win rate of challenges, then their challenge record would appear to be the same. However, when the marginal difference in win shares is calculated, the context of each of their respective challenges is properly considered. A comparison between Joe Anglim (season 38) and Frannie Marin (season 44) shows that both players had the same raw win rate on their respective seasons, with a 73% raw challenge win rate. Despite the fact that both players participated in eleven challenges and both won eight of them, Frannie had a significantly higher marginal win rate. Therefore, Frannie finished with a higher overall challenge performance rate.

Adjusted Challenge Performance Rates:
Since challenge performance is a rate statistic, calibration is required. The reason for this is because participating in one challenge isn't as informative about that player's skill as participating in ten challenges is. Just because a player wins one challenge, doesn't mean they will continue to win. So in addition to the average win rate that is calculated, a secondary adjusted rate is calculated to bring all players up to a baseline. The baseline that is used is the merge line. Merge line represents the collective group of players (from all seasons) that are eliminated immediately before and immediately after the merge. The average number of challenges participated in for all merge line players is 9.8478. The second number required is the average marginal difference for all players, which is zero. These numbers can be used to calculate the adjusted marginal difference, or the final challenge score.
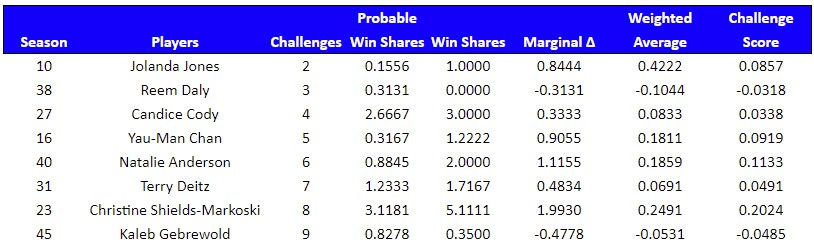
If a player has participated in 10 or more challenges, their score does not get adjusted. If they have participated in 9 challenges or less, then they get an adjustment up to 9.8478 maximum challenges participated in. For example, Jolanda Jones (season 10) participated in two challenges, one of which she won. Her probable win shares for those two challenges was .1556 (.1000 + .0556). Her marginal difference was .8444 (1.0000 - .1556). She was subsequently voted out of the game. Since she only participated in two challenges, her adjusted score is calculated as follows:
.4222 weighted average x 2 challenges = .8444 marginal difference
9.8478 maximum challenge baseline - 2 challenges = 7.8478
7.8478 adjusted maximum challenges x 0 average marginal difference = 0
.8444 marginal difference + 0 adjusted marginal difference = .8444
.8444 total marginal difference / 9.8478 maximum challenge baseline = .0857 adjusted marginal difference (otherwise referred to as challenge score)
Challenge Performance Rankings:
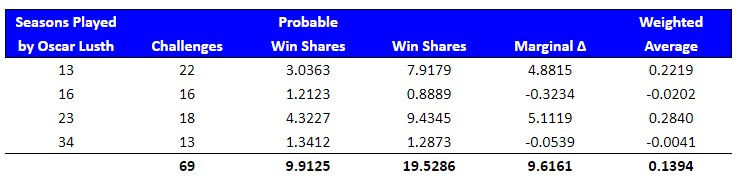
All individual challenge performance rates (and adjusted rates) for a player's entire game were calculated and ranked against the entire population of player games. A percentile rank was calculated for the ordinal rank. Oscar Lusth's season 13 challenge score of .2219 ranks him 5th overall our of 839 total player games, which fell into the 99.5 percentile.
Additionally, player ranking combines all the games each player has played into a single rate for their career. A percentile rank was calculated for the ordinal rank. Oscar Lusth's career challenge score of .1394 ranks him 15th overall out of 697 total players, which fell into the 97.9 percentile.
To view a full list of challenge performance rankings (both by season and career), please click the button below:
*** updated through season 46 ***

Comments